El plano cartesiano, también conocido como el plano euclidiano o sistema de coordenadas, es un sistema de referencias bidimensional formado por dos rectas infinitas perpendiculares entre sí, cuya intersección es denominada como el origen del sistema (0,0); ya que este punto es la referencia para ubicar cualquier otro punto en el plano.
Este sistema de coordenadas está conformado por dos rectas infinitas, una horizontal que es llamada como el eje de las abscisas o eje de las equis, y una recta vertical mundialmente conocida como el eje de las ordenadas o el eje de las ‘’y’’.

División del plano cartesiano
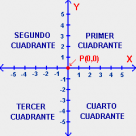
En el plano, al intersectarse las dos rectas perpendiculares, este es dividido en cuatro partes semejantes llamadas cuadrantes.
El primer y segundo cuadrante están ubicados en la parte superior del sistema, es decir, por encima del eje de las abscisas, uno a la derecha del eje de las ordenadas (primer cuadrante) y el otro ubicado por el lado izquierdo (segundo cuadrante).
En cambio, el tercer y cuarto cuadrante se encuentran por debajo del eje equis, abajo del segundo y primer cuadrante respectivamente.
Importancia del plano cartesiano
En el mundo de las matemáticas, esta es una herramienta básica, elemental y sumamente importante para cumplir con cualquiera de sus estudios o aplicaciones, un ejemplo es que en este plano se puede representar la gráfica de cualquier función.
Por otra parte, en el mundo de la física este plano puede ser usado para la representación de la posición de cualquier partícula.
Como fue dicho anteriormente, esta es una herramienta de vital importancia para el mundo actual, ya que es muy usada por los profesionales pertenecientes a cualquier área, como la ingeniería, arquitectura, derechos, contaduría y administración, entre muchos otros.

Obviamente no es usado de igual manera por todas esas ramas, sino que cada una tiene sus especificaciones de trabajo.
El hombre ha intentado hacer su vida más sencilla conforme han pasado los años. No es de extrañar que existan algunos sistemas más complejos que otros que puedan servir de referencia para distintos fines. En este pequeño artículo te hablaremos y explicaremos de forma breve lo que sería el plano cartesiano.
¿De qué se trata el plano cartesiano?
El plano cartesiano, o también llamado plano euclidiano, constituye un sistema referencial que está constituido por dos rectas numéricas, una es horizontal y la otra vertical. Estas rectas se unen, y cortan, en un punto específico.
La recta horizontal es conocida como el eje de las abscisas o de las “X”. La recta vertical es el conocido eje de las coordenadas o de las “Y”. El punto en que una recta pueda encontrarse en este plano se le denominará como origen.
Este plano se va creando dada la carencia de un sistema efectivo en el cual se pudieran representar vectores, puntos, figuras geométricas y otras tantas cosas que hoy podemos ver como sencillas. La precisión que estos elementos necesitan es de enorme relevancia al momento de deducir algunos cálculos, incluso, referentes a la astrología.
Función del plano cartesiano
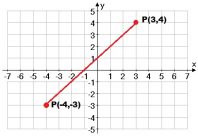
La finalidad primaria del plano cartesiano es la de trazar la posición de puntos, o zonas, que van a estar determinadas por sus coordenadas o pares ordenados.
Las coordenadas, pues, se formarán asociando un valor dado al eje de las abscisas y uno dado al eje de coordenadas.
Por otra parte, este sistema no se ha empleado únicamente para datos matemáticos o físicos, sino que ha sido de gran importancia en labores de ingeniería y arquitectura.
Una forma de este plano bastante utilizada es la parecida a una especie de mapa en la que se lleva a cabo un sistema de cuadrícula horizontal y vertical que describe la posición exacta de algo. Por ejemplo, esto se hace de gran importancia en personas que realizan constantes viajes en carretera.
¿Cómo se usa el plano cartesiano?
Para localizar puntos determinados en el plano cartesiano se tiene que contar cada unidad correspondiente en la dirección de la derecha en caso de que estas sean positivas. Si las unidades pertenecen a valores negativos, se deberá tomar en cuenta la dirección de la izquierda. Esto obviamente sobre el eje “X”.
Para utilizar el eje de “Y”, no existe mayor complicación, pues como podrás imaginar, para valores positivos se cuentan los valores de la parte de arriba. De darse el caso contrario, simplemente debes contar los valores de la parte inferior del eje.
La distancia que separa el punto en que se halla, por ejemplo, una persona, y el lugar al que se desea dirigir podrá ser representada a través del conocido plano euclidiano. El sitio origen será, pues, el lugar en el cual se encuentre el objeto, o persona, que se va a desplazar.
Ecuaciones
La ecuación correspondiente al eje “X” es “Y=0”, mientras que la referente al eje “Y” es, por tanto, “X=0”. Estas rectas, por sí solas, se encuentran en el punto 0, punto que significa el llamado origen. En consecuencia, tenemos que la coordenada inicial de dichas rectas es simplemente “(0,0)”.
Así, pues, las coordenadas de un punto cualquiera estarán determinadas por representaciones del segmento que alcanza desde el origen hasta la marca de cada eje.
En caso de que se cambien las escalas de los ejes en un factor “λ”, las coordenadas de un punto en el nuevo sistema pasarían a ser: “(x’,y’) = (λx, λy)”.
Cuadrantes
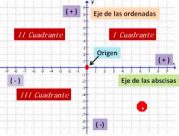
Cuando dos rectas se cortan entre sí, dividen el plano de coordenadas en cuatro regiones que son conocidas como cuadrantes. Aquí te mostramos la posición de cada una de estas zonas:
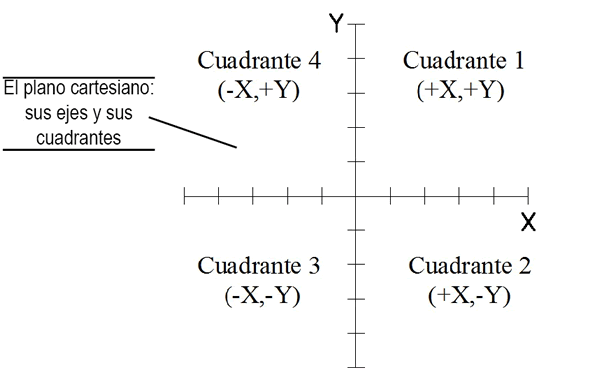
- Primer cuadrante: Región superior derecha.
- Segundo cuadrante: Región superior izquierda.
- Tercer cuadrante: Región inferior izquierda.
- Cuarto cuadrante: Región inferior derecha.
En geometría, este cuadrante se enumera desde el sentido contrario de las agujas del reloj. Se comienza entonces desde el cuadrante derecho superior.
En el primer cuadrante, todas las razones trigonométricas son positivas. En el segundo, las razones positivas serán solo el seno y la cosecante. En el tercer cuadrante, la tangente y la cotangente son las positivas. En el último cuadrante, el coseno y la secante son positivas.
De esta manera, el plano de coordenadas funciona al momento de calcular los ángulos que, por ejemplo, puede tener un determinado triángulo, así como otros problemas con esta connotación.
¿A qué se debe su nombre?
El nombre de este plano se debe a que fue realizado en honor a René Descartes, un grandísimo filósofo y matemático de nacionalidad francesa. Este, pues, fue el encargado de refinar aquellos detalles que faltaban por pulir en el sistema referencial de coordenadas.

Descartes optó por argumentar su pensamiento filosófico tomando un punto de partida manifiesto sobre el que construiría grandes conocimientos.
Ahora bien, como matemático y creador de lo que se conoce como geometría analítica, René también optó por tomar un punto de partida referencial, o sea, el sistema del que hablamos. Gracias a este pudo plasmar la geometría plana que emplea dos rectas que son perpendiculares y se cortan en algún punto.
Contexto histórico
Hay que tener en cuenta que los europeos no tenían la concepción del número cero para la época en la que todavía no habían llegado a América. Este precedente, inmediatamente, nos obliga a pensar en la importancia que tuvo Descartes para la ciencia europea en aquellos siglos.
Si ya la concepción del cero era nula, al momento de saber de su existencia, quizá gracias a los antiguos mexicanos, se les hizo sumamente complicado asimilar el hecho de que debían emplear números negativos. De hecho, en un principio, rechazaban por completo la posibilidad mencionada.
Algo bastante curioso y que quizá te resulte totalmente descabellado es que se cree que Descartes, en realidad, no llegó a emplear el plano de coordenadas del que te hablamos. El filósofo, pues, se refirió a las coordenadas en el sentido en que representaban las distancias de una curva.
Siendo Descartes un europeo nacido en el año 1596, podrás intuir que, para él, la utilización de números negativos también pudo haber parecido sin sentido. Este hecho, pues, nos puede hablar de los grandes pasos que ha dado la humanidad en general a lo largo de la historia de manera paulatina.
El plano cartesiano en física
La relevancia, debido a sus características, que tiene este plano referencial de coordenadas en la física es que ayuda a determinar la ubicación exacta de distintas partículas con respecto a otras.
Por otra parte, también ayuda a identificar y marcar el movimiento de alguna de las partículas. De igual modo, gracias a este sistema se puede calcular cualquier variación de velocidad o aceleración que se da en un determinado lapso de tiempo.
El plano cartesiano en matemática
La principal funcionalidad que tiene el plano cartesiano dentro del campo matemático es que permite representar gráficas de todo tipo de funciones.
Gracias a este instrumento se puede identificar la representación del movimiento de una función, así como otros datos referentes al desplazamiento.
Sin duda, esta herramienta ha sido una de las grandes invenciones que ha podido llevar a cabo el ser humano debido a su importancia y trascendencia temporal. No olvides compartir esta información con personas a las que les interese en mayor o menor medida el mundo de la ciencia.
Aprende más sobre el plano cartesiano