Una de las aplicaciones principales del plano cartesiano, es la del análisis matemático, siendo esta un área donde la representación de funciones es fundamental. Ya que, es necesario para poder identificar su comportamiento, clasificar a la función y entender el uso que esta puede llegar a tener.
Ahora bien, ¿Cómo se representa una función en el plano cartesiano?
Pues bastante sencillo representar curvas en el sistema cartesiano. Para ello, se requiere tener bien definidas las variables a trabajar, los puntos, el origen y el dimensionamiento de las escalas del plano cartesiano.
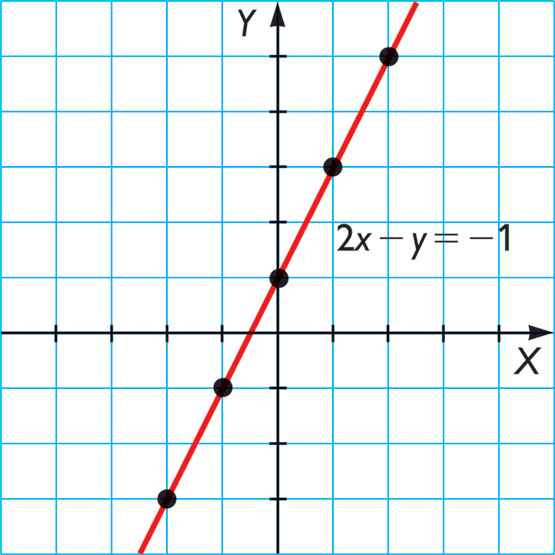
Curvas geométricas
Las funciones representadas en un plano, suelen ser denominadas curvas geométricas y pueden presentar diferentes formas. Las mismas, están directamente relacionadas al tipo de función que se esté trabajando. La cual, puede ser lineal, circular, exponencial, potencial, parabólica, entre otros.
¿Qué tienen en común todas esas funciones?
Bueno, para entender ¿Cómo se representa una función en el plano cartesiano? Es necesario identificar los elementos fundamentales de una función. Los cuales empiezan con una ecuación característica, donde se ubican las variables, siendo una de ellas dependiente de la otra. También, están los puntos de origen que irán definiendo el comportamiento de la curva.
variables
Las variables de una función se suelen representar con a las letras “X” y “Y”, donde la X se denomina abscisa y la Y se denomina ordenada. Estas en conjunto representan las coordenadas de cada uno de los puntos de la curva y se obtienen sustituyendo sus valores en la ecuación característica de cada función.
Entonces, al tener las variables para ambos ejes definidas y la ecuación característica de la curva, solo hace falta plasmar los puntos en el plano. Una vez realizada dicha tarea, se unen en secuencia los puntos y se logra conseguir la curva de la función deseada. Lo cual, permite dar por solventada la incógnita de ¿Cómo se representa una función en el plano cartesiano?

 Tabulación y variación en el plano cartesiano
Tabulación y variación en el plano cartesiano Área de un polígono en el plano cartesiano
Área de un polígono en el plano cartesiano Plano cartesiano en blanco
Plano cartesiano en blanco Partes de un plano cartesiano
Partes de un plano cartesiano Punto de origen en el plano cartesiano
Punto de origen en el plano cartesiano ¿Cómo representar vectores en el plano cartesiano?
¿Cómo representar vectores en el plano cartesiano? Diferencia entre plano cartesiano y plano euclidiano
Diferencia entre plano cartesiano y plano euclidiano Diferencia entre producto cartesiano y plano cartesiano
Diferencia entre producto cartesiano y plano cartesiano