¿Qué es una abscisa en un plano?

En el extenso mundo de la geometría, es posible encontrarse con el importante sistema cartesiano. El cual, es una herramienta que permite realizar representaciones geométricas en un sistema de dos dimensiones. El mismo se compone de un plano, donde se ubican puntos de manera ordenada con la ayuda de los ejes coordenados.

Dichos ejes son rectos, pero se representan de manera diferente porque uno presenta una orientación vertical y el otro una horizontal.

Los mismos, poseen una escala a convenir para poder ubicar los puntos y realizar las representaciones necesarias. Así que, presta atención para que puedas resolver la incógnita de ¿Qué es una abscisa en un plano?

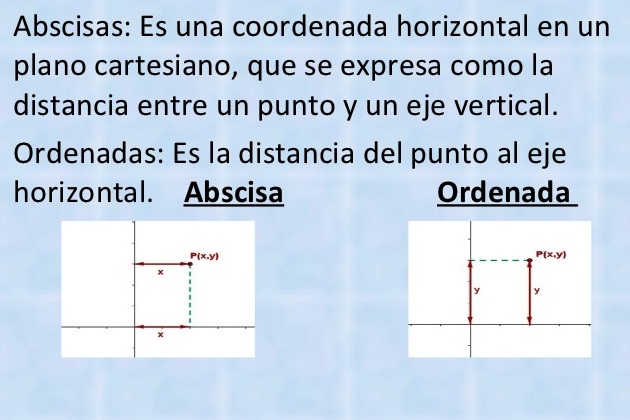
La abscisa

Para muchas personas es confuso trabajar en un plano de coordenadas, debido a que siempre se presenta la duda de ¿Qué es una abscisa en un plano? O el mismo caso, pero con las ordenadas.

Ahora bien, cuando se habla de las abscisas, se habla de una coordenada en el plano cartesiano. Específicamente, se hace referencia a la coordenada que va relacionada al eje horizontal y representa la distancia existente en el origen y un punto en específico.

Coordenadas

Las coordenadas en el Sistema cartesiano, son valores que ubican un punto en el plano y se conforma de dos componentes. Una de ellas, será la que represente la distancia entre el origen y el punto con respecto al eje horizontal, siendo estas las ordenadas. La otra coordenada, será la abscisa y representará la distancia del eje vertical hasta el punto.

Simbología de las componentes

En el mundo de las matemáticas se utilizan diversas simbologías para tratar diversas variables matemáticas. En este caso, a las ordenadas se les suele denotar con la letra “Y”, mientras que, a las abscisas se les denota con una letra “X”.

Entonces, definitivamente no será necesario volver a preguntar ¿Qué es una abscisa en un plano? Ya que te lo hemos explicado muy bien, tanto que podrías explicárselo a tus amigos si se les presente esta misma incógnita.