Ángulos positivos y negativos en el plano cartesiano

Las representaciones que se pueden realizar en el plano cartesiano son realmente variadas y entre ellas es posible ubicar a los ángulos. Los cuales, son elementos fundamentales para poder trabajar con figuras y curvas inclinadas con respecto a los ejes coordenados del plano.

Los ángulos suelen tener como referencia una recta que gira en torno al origen del sistema cartesiano.

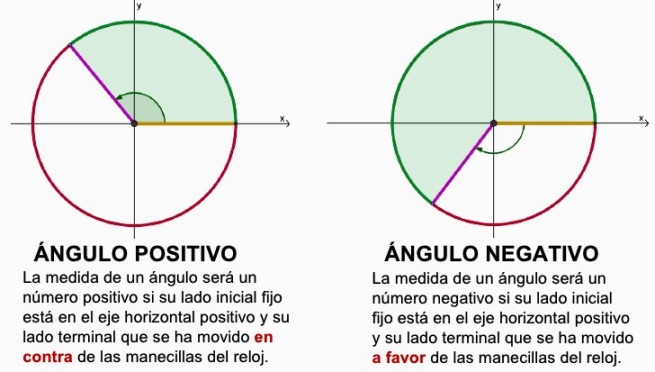
De hecho, el mencionado giro será fundamental para determinar el signo que tendrá el ángulo a trabajar. Ya que, el sentido de giro permite identificar los ángulos positivos y negativos en el plano cartesiano.

Sentido de giro

Para trabajar con los ángulos en el plano cartesiano, es necesario poner a girar una recta con respecto al eje coordenado y seguir un punto fijo de su trayectoria. De esa manera es posible identificar el ángulo con el cual se está trabajando en cada caso. Sin embargo, hay un factor determinante en todo esto y es el sentido que tenga el giro en el plano.

Ya que, los ángulos positivos y negativos en el plano cartesiano se definen exclusivamente por el sentido de giro que se emplee.

Ángulos positivos

Identificar los ángulos positivos es realmente sencillo, ya que solo hace falta identificar los ángulos con giros en sentido anti horario. Además, es importante acotar que magnitud de dicho ángulo se toma desde el eje de las abscisas hasta el punto en la recta más cercano al seguir el giro en el sentido mencionado.

Ángulos negativos

Los ángulos negativos son aquellos cuyo giro se realiza con un sentido horario, tomando como referencia el eje de las abscisas. Su magnitud será la existente entre el eje ya mencionado y el punto de la gráfica más cercano en el sentido de las agujas del reloj.

En conclusión, es bastante sencillo identificar los ángulos positivos y negativos en el plano cartesiano. Solo hace falta prestar un poco de atención para poder identificarlos y trabajarlos correctamente.